【Java】フラクタル図形を描画してみよう
フラクタル図形を描きたいというコメントをいただいて、フラクタル図てなんだ?って気になったのでちょっと勉強しました。にわかなのですが一応記事にしとこうかなと思います。
フラクタル図ってなんだ?
フラクタル図形とは、図形の部分と全体が自己相似(再帰)になっているものなどをいう。…とwikiに書いてありました。
相似っていうのは、ある図形を拡大縮小し、もう一方の図形と重ね合わせられような図形を言います。
これは中学か高校かの数学で習いましたよね?
それら相似の性質を利用してゴリゴリ再帰処理させて描いたのがフラクタル図なのかな?
フラクタル図を描く際に必要な知識とか
まずはフラクタル図を描く際に必要な知識は何かを考えてみました。
再帰処理
再帰処理は実行している関数、メソッドの中から自分自身の関数、メソッドを呼び出すような処理を言います。
再帰処理をうまく使えば単純な記述で目的の処理が書ける事例もたくさんあります。私の経験ではフォルダ階層制御、構文解析、経路探索で使用する機会がありました。
再帰処理は普通のお仕事でも役に立つ可能性がありますので必ず覚えておきましょう。
再帰処理を解説してるサイトへのリンクも貼っておきます。
もちろんフラクタル図は再帰処理をゴリゴリ使いますので必要になります。for文でもできますが再帰処理のほうがプログラムが単純になることは間違いないです。
描画APIをうまく活用する
描画APIをうまく活用すると表現の幅が広がりそうです。特にPathを使った方法を覚えておけばいろいろなことができそうですね。
あとはAffineTransformなどを利用すれば回転やスケール変換もやりやすいので、私みたいな計算が苦手な人はうまく活用すると良さそう。
これらのAPIは既に他の記事で紹介しているので参考にしてください。
下記の記事は画像ベースに紹介していますが、描画APIすべてにAffineTransformは使えます。またdeltaTransformという座標を引き渡して変換するメソッドも存在しますのでこれの存在も頭の片隅に置いておけば使える機会があるかもしれません。
ある程度の数学の知識があれば有利
やはり特定の座標を求めたりする際には必要な場合が多々ありますね。
私も数学は超苦手なのですが、sin関数cos関数だけはなんとか少し使えるようにはなっています。
これだけでも役に立つので、まずはsin関数cos関数の使い方から勉強してみてはどうでしょうか。
発想力も必要?
こんな図形を描きたいなと想像して数式と再帰処理を組み立てられればフラクタルマスターになれそう。
ただ、意外と適当に遊んでるだけでもおもしろい図形が作れたりするので適当に遊んでみるのもいいとおもいます。
むしろ適当に遊んでたほうがいいかもしれません。
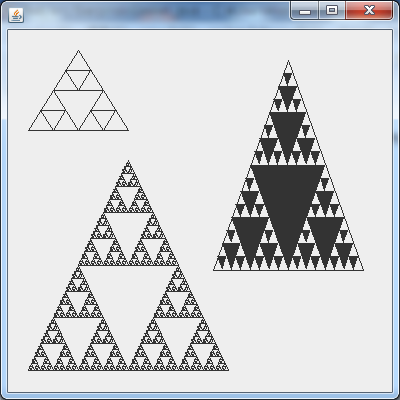
シェルピンスキーのギャスケットを描いてみる
ではフラクタル図で最も簡単そうなシェルピンスキーのギャスケットの図を描いてみます。
この図は三角形の中に小さな三角形を描き、描いた三角形の中にさらに小さな三角形を描いていき・・・ていうのをひたすら繰り返すだけでできる単純なものです。
解説は面倒なので今回私が参考にさせていただいたプログラムが掲載されているqiitaの記事を紹介しておきます。
では記事を参考にちょっと手を加えてシェルピンスキーのギャスケットを描画するメソッドを作ってみます。
プログラム中には何をしているかのコメントを書いておいたのでそれも参考にしてみてください。
import java.awt.Graphics;
import javax.swing.JFrame;
import javax.swing.JPanel;
class FractalUtil{
/**
* シェルピンスキーのギャスケットの図形を描画するメソッド
* 引数には矩形データを引き渡し、その矩形に収まるように描画します。
* @param g 描画オブジェクト
* @param x 描画する左の座標
* @param y 描画する上の座標
* @param w 描画幅
* @param h 描画高さ
* @param fineness きめ細かさ
*/
public static void drawSierpinskiGasket(Graphics g, int x, int y, int w, int h, int fineness) {
_drawSierpinskiGasketStart(g,x,y,w,h,fineness,false);
}
/**
* シェルピンスキーのギャスケットの図形を中塗り描画するメソッド
* 引数には矩形データを引き渡し、その矩形に収まるように描画します。
* @param g 描画オブジェクト
* @param x 描画する左の座標
* @param y 描画する上の座標
* @param w 描画幅
* @param h 描画高さ
* @param fineness きめ細かさ
*/
public static void fillSierpinskiGasket(Graphics g, int x, int y, int w, int h, int fineness) {
_drawSierpinskiGasketStart(g,x,y,w,h,fineness,true);
}
//大枠の三角形を描画し、再帰処理を開始するメソッド
private static void _drawSierpinskiGasketStart(Graphics g, int x, int y, int w, int h, int fineness, boolean isFill) {
if ( fineness <= 0 ) throw new IllegalArgumentException("recursive is 1 or more.");
//引数の矩形に収まる三角形を描画するための3点を求める
//三角形の上の頂点
int x1 = x + w / 2;
int y1 = y;
//三角形の右下の頂点
int x2 = x + w;
int y2 = y + h;
//三角形の左下の頂点
int x3 = x;
int y3 = y + h;
//三角形を描画
g.drawPolygon(new int[] {x1, x2, x3},new int[] {y1, y2, y3}, 3);
//きめ細かさを減算
fineness--;
//ベースとなる三角形の頂点を引き渡し再帰処理を開始
_drawSierpinskiGasket(g,x1,y1,x2,y2,x3,y3,fineness,isFill);
}
//引数には元の三角形の三点を指定
//出来た三角形の各辺の中心点を算出し、新たな三角形を描画するメソッド
//finenessが0以上の場合は元の三角形と作成した三角形によりできた図形の上、右、左にそれぞれ新たな子三角形を作成するように要求する
private static void _drawSierpinskiGasket(Graphics g, int x1, int y1, int x2, int y2, int x3, int y3, int fineness, boolean isFill) {
//ベースの三角形のそれぞれの辺の中点を算出します。
//右側の辺の中点
int x12 = (x2 + x1) / 2;
int y12 = (y2 + y1) / 2;
//底辺の中点
int x23 = (x3 + x2) / 2;
int y23 = (y3 + y2) / 2;
//左側の辺の中点
int x31 = (x1 + x3) / 2;
int y31 = (y2 + y1) / 2;
//それぞれの中点を結ぶ三角形を描画
if ( isFill ) {
g.fillPolygon(new int[] {x12, x23, x31},new int[] {y12, y23, y31}, 3);
} else {
g.drawPolygon(new int[] {x12, x23, x31},new int[] {y12, y23, y31}, 3);
}
//きめ細かさ(再帰回数が残っている場合は子三角を作成させる。)
if ( fineness > 0 ) {
fineness--;
//描画した三角形により新たに上、右下、左下に三角形ができるのでそれに対してまた三角形を描画するように要求します。(再帰処理)
_drawSierpinskiGasket(g,x1,y1,x12,y12,x31,y31,fineness,isFill);//上側三角に子三角を作成させる。引数には上側三角形の頂点を引き渡す
_drawSierpinskiGasket(g,x12,y12,x2,y2,x23,y23,fineness,isFill);//右下側三角に子三角を作成させる。引数には右下側三角形の頂点を引き渡す
_drawSierpinskiGasket(g,x31,y31,x23,y23,x3,y3,fineness,isFill);//左下側三角に子三角を作成させる。引数には左下側三角形の頂点を引き渡す
}
}
}
public class SierpinskiGasket extends JFrame {
public static void main(String[] args) {
new SierpinskiGasket();
}
SierpinskiGasket(){
//シェルピンスキーのギャスケットの図形をウィンドウ上に描画するサンプルプログラムを実行する
JPanel p = new JPanel() {
@Override
public void paint(Graphics g) {
//シェルピンスキーのギャスケットの図形を描画
//drawSierpinskiGasket(Graphicsオブジェクト,x座標,y座標,幅,高さ,きめ細かさ)
FractalUtil.drawSierpinskiGasket(g, 20, 20, 100, 80, 2);
FractalUtil.drawSierpinskiGasket(g, 20, 130, 200, 210, 6);
FractalUtil.fillSierpinskiGasket(g, 205, 30, 150, 210, 4);//塗りつぶしの場合はfillSierpinskiGasketを実行
}
};
add(p);
setSize(400,400);
setDefaultCloseOperation(EXIT_ON_CLOSE);
setVisible(true);
}
}
オリジナルでフラクタルっぽい何かを描いてみる
最後に私が今回学んだことをベースにして作ったフラクタルのプログラムを紹介して終わりたいと思います。
何をしているかはコード内のコメントを参考にしてください。
ただ・・・残念ながら私はいろいろ知識不足でかつ発想力もないのでありきたりな物しか作れませんでした。
PathやAffineTransformを利用したパターンも用意してます。
何かの参考になったらいいなあ・・・
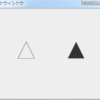
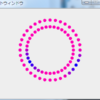
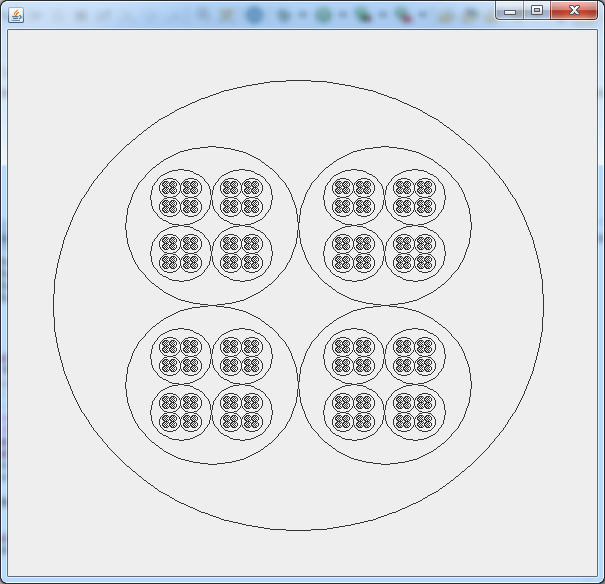
一つ目は円の中に円を描くだけという超簡単なサンプルです。
import java.awt.Graphics;
import javax.swing.JFrame;
import javax.swing.JPanel;
public class FractalTest extends JFrame{
public static void _drawOrgFractal(Graphics g, int x, int y, int w, int h, int f) {
//指定矩形を4分割した矩形内に収まる楕円を4つ描く
int rw = w/2;
int rh = h/2;
g.drawOval(x,y,rw,rh);
g.drawOval(x+rw,y,rw,rh);
g.drawOval(x,y+rh,rw,rh);
g.drawOval(x+rw,y+rh,rw,rh);
f--;
if ( f >= 0 ) {
//4つ描いた楕円のうちの一つの楕円の高さと幅の半分を求める
int crw = rw/2;
int crh = rh/2;
//4つの楕円の中心点
int cx = x + rw;
int cy = y + rh;
//4つ描いた楕円のうちの右下に位置する楕円の中心点を求める
int ccx = cx + crw;
int ccy = cy + crh;
//4つのうち右下描いた楕円に収まる矩形の幅と高さの半分の値を算出
int cmx = (int) (Math.cos(Math.toRadians(45))*crw);
int cmy = (int) (Math.sin(Math.toRadians(45))*crh);
//4つのうち右下描いた楕円に収まる矩形の幅と高さ
int cw = cmx * 2;
int ch = cmy * 2;
//楕円の中にさらに4つの楕円を描画する
_drawOrgFractal(g,ccx-cmx-rw,ccy-cmy-rh,cw,ch,f);//左上の円の中に納まる矩形を引き渡し4つの円を描画するように再起呼び出し
_drawOrgFractal(g,ccx-cmx-rw,ccy-cmy,cw,ch,f);//左下の円の中に納まる矩形を引き渡し4つの円を描画するように再起呼び出し
_drawOrgFractal(g,ccx-cmx,ccy-cmy-rh,cw,ch,f);//右上の円の中に納まる矩形を引き渡し4つの円を描画するように再起呼び出し
_drawOrgFractal(g,ccx-cmx,ccy-cmy,cw,ch,f);//右下の円の中に納まる矩形を引き渡し4つの円を描画するように再起呼び出し
}
}
public static void drawOrgFractal(Graphics g, int x, int y, int w, int h, int f) {
if ( f <= 0 ) throw new IllegalArgumentException();
//ベースとなる楕円を描く
g.drawOval(x,y,w,h);
//幅、高さの半分を算出
int rw = w/2;
int rh = h/2;
//楕円の中心点
int cx = x + rw;
int cy = y + rh;
//描いた楕円に収まる矩形の幅と高さの半分の値を算出
int cmx = (int) (Math.cos(Math.toRadians(45))*rw);
int cmy = (int) (Math.sin(Math.toRadians(45))*rh);
//描いた楕円に収まる矩形の幅と高さ
int cw = cmx * 2;
int ch = cmy * 2;
f--;
//指定矩形の中に4つの楕円を描く再帰処理を開始
_drawOrgFractal(g,cx-cmx,cy-cmy,cw,ch,f);
}
public static void main(String[] args) {
new FractalTest();
}
FractalTest(){
add(new JPanel() {
public void paint(Graphics g) {
//指定矩形に収まる楕円を描く
drawOrgFractal(g,45,50,490,450,5);
}
});
setSize(600,600);
setDefaultCloseOperation(EXIT_ON_CLOSE);
setVisible(true);
}
}
ただのおまんじゅうですありがとうございます。
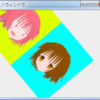
次は扇形っぽいものを描画してそこからさらに回転させながら扇形を描画していくだけのサンプルです。
PathやAffineTransformも使ったサンプルとして作成しましたが、計算量が増えてしまって気持ち悪いコードになりました。
回転もAffineTransform使ったほうがすんなり終わったかもしれませんね。
import java.awt.Color;
import java.awt.Graphics;
import java.awt.Graphics2D;
import java.awt.geom.AffineTransform;
import java.awt.geom.GeneralPath;
import javax.swing.JFrame;
import javax.swing.JPanel;
public class FractalTest extends JFrame{
public static void drawOrgFractal2(Graphics g, int x, int y, int w, int h, int angle, int distance, int f) {
if ( f <= 0 ) throw new IllegalArgumentException();
int rw = w/2;
int rh = h/2;
int cx = x + rw;
int r = x+w;
int b = y+h;
Color clr = g.getColor();
//扇形の頂点となる三点を引数に渡す
drawOrgFractal2(g,cx,y,r,b,x,b,angle,distance,f,clr, new AffineTransform());
g.setColor(clr);
}
public static void drawOrgFractal2(Graphics g, int x1, int y1, int x2, int y2, int x3, int y3, int angle, int distance, int f, Color clr, AffineTransform at) {
g.setColor(clr);
//三点の底辺となる辺の中心点を求める
int bcx = x2 + (x3-x2) / 2;
int bcy = y2 + (y3-y2) / 2;
//底辺の中心点から角のある頂点までのベクトルを求める
int vx = bcx - x1;
int vy = bcy - y1;
//底辺の中心点から扇形の角のある頂点までの距離を求める
double d = (int) Math.sqrt(vx*vx+vy*vy);
//扇形の角のある頂点から底辺の中心点への角度のラジアンを求める
double rad = Math.atan2(vy,vx);
//扇形を描画する
GeneralPath p = new GeneralPath();
p.moveTo(x1, y1);
p.lineTo(x2, y2);
p.curveTo(x2, y2, bcx+Math.cos(rad)*(d*0.2), bcy+Math.sin(rad)*(d*0.2), x3, y3);
p.closePath();
Graphics2D g2 = (Graphics2D)g;
g2.setTransform(at);
g2.draw(p);
//これは上側に付ける飾りとして描画
g.drawOval(x1-2, y1-2, 4, 4);
f--;
if ( f >= 0 ) {
//角のある頂点から第二頂点へのベクトルを求める
int vx12 = x2 - x1;
int vy12 = y2 - y1;
//角のある頂点から第三頂点へのベクトルを求める
int vx13 = x3 - x1;
int vy13 = y3 - y1;
//角のある頂点から第二頂点への距離を求める(二等辺などでもう一方d13は求めずにd12を使いまわす)
int d12 = (int) Math.sqrt(vx12*vx12+vy12*vy12);
//角のある頂点から第二頂点への角度
double rad12 = Math.atan2(vy12,vx12);
//角のある頂点から第三頂点への角度
double rad13 = Math.atan2(vy13,vx13);
//扇形を傾ける角度
double baseRad = Math.toRadians(angle);
//スケール変換(縮小)
//再帰するごとに小さくなるように調整
AffineTransform cat = new AffineTransform();
cat.translate(bcx, bcy);
cat.scale(at.getScaleX()*0.9, at.getScaleY()*0.9);
cat.translate(-bcx, -bcy);
//新しく作成する扇形をbaseRad分右に回転させるためのラジアン
double rrad = Math.toRadians(-180) + rad + baseRad;
//右上に作成する扇形の角頂点
int rx1 = (int) (Math.cos(rrad) * distance + bcx);
int ry1 = (int) (Math.sin(rrad) * distance + bcy);
//右上に作成する扇形の第二頂点
int rx2 = (int) (Math.cos(baseRad+rad12) * d12 + rx1);
int ry2 = (int) (Math.sin(baseRad+rad12) * d12 + ry1);
//右上に作成する扇形の第三頂点
int rx3 = (int) (Math.cos(baseRad+rad13) * d12 + rx1);
int ry3 = (int) (Math.sin(baseRad+rad13) * d12 + ry1);
//扇形を描画
drawOrgFractal2(g,rx1,ry1,rx2,ry2,rx3,ry3,angle,distance,f,clr.brighter(),cat);
//スケール変換(縮小)
cat.setToIdentity();
cat.translate(bcx, bcy);
cat.scale(at.getScaleX()*0.9, at.getScaleY()*0.9);
cat.translate(-bcx, -bcy);
//新しく作成する扇形をbaseRad分左に回転させるためのラジアン
double lrad = Math.toRadians(180) + rad - baseRad;
//左上に作成する扇形の角頂点
int lx1 = (int) (Math.cos(lrad) * distance + bcx);
int ly1 = (int) (Math.sin(lrad) * distance + bcy);
//左上に作成する扇形の第二頂点
int lx2 = (int) (Math.cos(-baseRad+rad12) * d12 + lx1);
int ly2 = (int) (Math.sin(-baseRad+rad12) * d12 + ly1);
//左上に作成する扇形の第三頂点
int lx3 = (int) (Math.cos(-baseRad+rad13) * d12 + lx1);
int ly3 = (int) (Math.sin(-baseRad+rad13) * d12 + ly1);
drawOrgFractal2(g,lx1,ly1,lx2,ly2,lx3,ly3,angle,distance,f,clr.brighter(),cat);
}
}
public static void main(String[] args) {
new FractalTest();
}
FractalTest(){
add(new JPanel() {
public void paint(Graphics g) {
g.setColor(Color.BLACK);
g.fillRect(0, 0, 1160, 1000);
g.setColor(new Color(50,70,10));
//指定矩形に収まる三点を元に扇形っぽいものを作成する
drawOrgFractal2(g,565,580,60,80,20,130,12);
}
});
setSize(1160,1000);
setDefaultCloseOperation(EXIT_ON_CLOSE);
setVisible(true);
}
}
なんかわけのわからないコメントだな・・・ひどい・・・てかもっと簡単な計算方法あったんだろうな・・・処理効率もあんま考えてないです。
もうちょっとすげえきれいってなるような図形が作りたかったんだけどね。なーんか汚いんよねぇ。
フラクタル弄る機会があってもっとやばいのができたらまた追記しようかなと思いますが、多分そんな機会ないですね。
あとこういうプログラム組むときできるだけdoubleで計算したほうが良いですね。小数点切り捨てでずれてしまう。



![再帰関数 (1) | じっくり学ぶ Java講座 [初心者向け・入門]](https://nompor.com/wp-content/themes/luxeritas/images/no-img-100x100.png)









ディスカッション
コメント一覧
まだ、コメントがありません